Ejemplos de integrales definidas
Integral definida
La integral definida es el área bajo la gráfica de una función delimitada en un intervalo [A,B] para el eje X y comenzando desde Y=0 para dicho eje. La integral definida se representa por una S alargada o símbolo de integral, una variable a en la parte baja de la S que representa el límite inferior de integración y por una variable b que representa el límite superior de la integración.
Una función f(x) representa la función a integrar y dx que se llama diferencial de x que representa el integrando o variable sobre la cual se realizará la integración.
Las integrales definidas mantienen ciertas propiedades o características como por ejemplo: el valor de la integral de [A a B] cambia de signo si se invierten los intervalos [B a A], si los límites de integración son iguales, entonces el valor de la integral vale 0. Si la integral se parte en un punto medio de A a C y de C a A, la suma de resultados es lo mismo que integrar de A a B. Si una función está compuesta por alguna suma o resta esta puede ser dividida en las sumas o restas respectivamente dicha función y dicha suma de integrales tendrá el mismo valor de la integral de la función completa.
Ejemplo de integrales definidas
- Integral 1
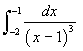
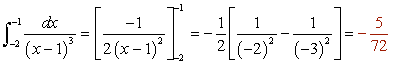
- Integral 2
![]()
![]()
- Integral 3
![]()
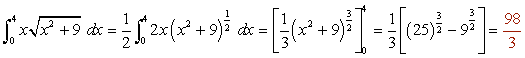
- Integral 4
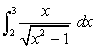
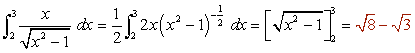
- Integral 5
![]()
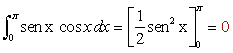
- Integral 6
![]()
![]()
- Integral 7
![]()
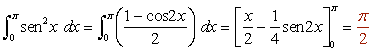
- Integral 8
![]()
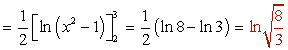
- Integral 9
![]()
![]()
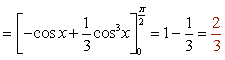
- Integral 10
![]()
![]()
Reglas de las integrales definidas
- Toda integral extendida a un intervalo de un solo punto, [a, a], es igual a cero.
- Cuando la función f (x) es mayor a cero, su integral es positiva. Si la función es menor que cero, su integral es negativa.
- La integral de una suma de funciones es igual a la suma de sus integrales tomadas por separado.
- La integral del producto de una constante por una función es igual a la constante por la integral de la función (es decir, se puede «sacar» la constante de la integral).
- Al permutar los límites de una integral, ésta cambia de signo.